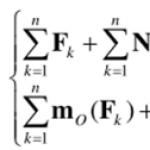D'Alemberti teoreetilise mehaanika põhimõte. Kuidas sõnastada d'Alemberti põhimõte Mis on d'Alemberti põhimõte

Kui materiaalne punkt liigub, on selle kiirendus igal ajahetkel selline, et punktile rakenduvad etteantud (aktiivsed) jõud, seoste reaktsioonid ja fiktiivne d'Alemberti jõud Ф = - м moodustavad tasakaalustatud jõudude süsteemi.

Tõestus. Vaatleme mittevaba ainelise punkti liikumist massiga T inertsiaalses võrdlusraamis. Dünaamika põhiseaduse ja seostest vabanemise põhimõtte kohaselt on meil:

kus F on antud (aktiiv)jõudude resultant; N on kõigi punktile rakendatud sidemete reaktsioonide tulemus.

Seda on lihtne (13.1) teisendada järgmisele kujule:

Vektor Ф = - et nimetatakse d'Alemberti inertsijõuks, inertsijõuks või lihtsalt D'Alemberti jõud. Allpool kasutame ainult viimast terminit.

Nimetatakse võrrandit (13.3), mis väljendab d'Alemberti printsiipi sümboolsel kujul kinetostaatiline võrrand materiaalne punkt.

Mehaanilise süsteemi (süsteem P materiaalsed punktid).

Kellelegi To mehaanilise süsteemi punktis on võrdsus (13.3) täidetud:

Kus ? Kellele - antud (aktiivsete) jõudude resultant To punkt; N Kellele - pealesunnitud sidemete reaktsioonide tulemus k-th punkt; F k = - seega k- D'Alemberti jõud To punkt.

On ilmne, et kui tasakaalutingimused (13.4) on täidetud jõudude F*, N* : , Ф* iga kolmiku korral (Sellele = 1,. .., P), siis kogu süsteem 3 P tugevus

on tasakaalus.

Järelikult, kui mehaaniline süsteem igal ajahetkel liigub, moodustavad sellele rakenduvad aktiivsed jõud, ühenduste reaktsioonid ja süsteemi punktide D'Alemberti jõud tasakaalustatud jõudude süsteemi.

Süsteemi (13.5) jõud ei ole enam koonduvad, seetõttu, nagu on teada staatikast (punkt 3.4), on selle tasakaalu jaoks vajalikud ja piisavad tingimused järgmisel kujul:

Võrrandeid (13.6) nimetatakse mehaanilise süsteemi kinetostaatilisteks võrranditeks. Arvutusteks kasutatakse nende vektorvõrrandite projektsioone momendipunkti läbivatele telgedele KOHTA.

Märkus 1. Kuna süsteemi kõigi sisejõudude summa ja ka nende momentide summa mis tahes punkti suhtes on võrdne nulliga, siis võrrandites (13.6) piisab, kui võtta arvesse ainult reaktsioone. välisedühendused.

Kinetostaatilisi võrrandeid (13.6) kasutatakse tavaliselt mehaanilise süsteemi ühenduste reaktsioonide määramiseks, kui süsteemi liikumine on antud ja seetõttu on teada süsteemi punktide kiirendused ja neist sõltuvad D'Alemberti jõud. .

Näide 1. Otsige üles tugireaktsioonid A Ja IN võll, kui see pöörleb ühtlaselt sagedusega 5000 p/min.

Punktmassid on võlliga jäigalt ühendatud gp= 0,1 kg, t 2 = 0,2 kg. Suurused teada AC - CD - DB = 0,4 m, h= 0,01 m. Võlli massi peetakse tühiseks.

Lahendus. D'Alemberti põhimõtte kasutamiseks kahest punktmassist koosneva mehaanilise süsteemi puhul märgime diagrammile (joonis 13.2) etteantud jõud (raskusjõud) Gi, G 2, reaktsioonireaktsioonid N4, N# ja D'Alemberti jõud Ф |, Ф 2.

D'Alambsrovi jõudude suunad on vastupidised punktmasside kiirendustele T b t 2u mis kirjeldavad ühtlaselt raadiusega ringe hümber telje AB võll

Leiame gravitatsiooni ja Dalambrovi jõudude suurused:

Siin on võlli nurkkiirus kaas- 5000* l/30 = 523,6 s Kinetostaatiliste võrrandite (13,6) projitseerimine Descartes'i telgedele Ah, ah, Az, saame paralleeljõudude Gi, G 2, 1Чд, N tf, Фь Ф 2 tasapinnalise süsteemi tasakaalu tingimused:

Alates hetke võrrandist, mille me leiame N sisse = - + - 1 - - - 2 --- =

(0,98 + 274) 0,4 - (548 -1,96) 0,8 w „

272 N ja projektsioonivõrrandist peale

telg Jah: Na = -NB +G,+G2 +F,-F2 = 272 + 0,98 +1,96 + 274-548 =0,06 N.

Kinetostaatilisi võrrandeid (13.6) saab kasutada ka süsteemi liikumise diferentsiaalvõrrandite saamiseks, kui need on koostatud nii, et kitsendusreaktsioonid on elimineeritud ja selle tulemusena on võimalik saada kiirenduste sõltuvus etteantud. jõud.

Inertsjõud materiaalse punkti ja mehaanilise süsteemi dünaamikas

Inertsi jõul Materiaalne punkt on punkti massi ja selle kiirenduse korrutis miinusmärgiga, st dünaamika inertsiaaljõud rakenduvad järgmistel juhtudel:

• 1. Uurides ainelise punkti liikumist sisse mitteinertsiaalne(liikuv) koordinaatsüsteem, st suhteline liikumine. Need on transpordi- ja Coriolise inertsijõud, mida sageli nimetatakse Euleri jõududeks.
• 2. Dünaamikaülesannete lahendamisel kinetostaatilisel meetodil. See meetod põhineb d’Alemberti printsiibil, mille kohaselt teatud kiirendusega liikuva materiaalse punkti või materiaalsete punktide süsteemi inertsiaaljõud inertsiaalne võrdlussüsteem. Neid inertsiaaljõude nimetatakse d'Alemberti jõududeks.
• 3. D'Alemberti inertsiaaljõude kasutatakse ka dünaamika ülesannete lahendamisel Lagrange-D'Alemberti printsiibi või dünaamika üldvõrrandi abil.

Avaldis projektsioonides ristkoordinaatide telgedel

Kus - ristkoordinaatide telje punkti kiirenduse projektsioonide moodulid.

Kui punkt liigub kõverjoonelises suunas, saab inertsiaaljõu lagundada puutujaks ja normaaljõuks:; , - tangentsiaalse ja normaalkiirenduse moodul; - trajektoori kõverusraadius;

V- punkti kiirus.

D'Alemberti põhimõte materiaalse punkti jaoks

Kui mittevabaks materiaalne punkt, mis liigub rakendatud aktiivjõudude ja ühenduste reaktsioonijõudude toimel, rakendab oma inertsijõudu, siis tekib igal ajahetkel tekkinud jõudude süsteem tasakaalus, st nende jõudude geomeetriline summa on võrdne nulliga.

mehaaniline punktkorpuse materjal

Kus - punktile rakendatud aktiivjõudude resultant; - punktile peale pandud sidemete reaktsioonide tulemus; materiaalse punkti inertsjõud. Märkus. Tegelikult ei rakendata materiaalse punkti inertsiaaljõudu mitte punktile endale, vaid kehale, mis annab sellele punktile kiirenduse.

D'Alemberti põhimõte mehaanilise süsteemi jaoks

Geomeetriline summa süsteemile mõjuvate välisjõudude peamised vektorid ja süsteemi kõikide punktide inertsjõud, samuti nende jõudude põhimomentide geomeetriline summa mingi keskpunkti suhtes mittevaba mehaanilise süsteemi jaoks igal ajahetkel on võrdsed nulliga, st.

Jäiga keha inertsjõudude peavektor ja peamoment

Süsteemi punktide peavektor ja inertsjõudude põhimoment määratakse iga antud mehaanilises süsteemis sisalduva jäiga keha jaoks eraldi. Nende definitsioon põhineb staatikast tuntud Poinsot' meetodil, mis viib suvalise jõudude süsteemi antud keskmesse.

Selle meetodi alusel saab keha kõigi punktide inertsiaaljõud, üldjuhul selle liikumised viia massikeskmesse ja asendada põhivektori * ja põhimomendiga. massikeskme suhtes. Need määratakse valemitega st mis tahes jäiga keha liikumisel on inertsiaalsete jõudude peavektor miinusmärgiga võrdne keha massi ja keha massikeskme kiirenduse korrutisega; , Kus r kc -- raadiuse vektor k-th punktid, mis on tõmmatud massikeskmest. Need valemid jäiga keha liikumise erijuhtudel on kujul:

1. Edasi liikumine.

2. Keha pöörlemine ümber massikeskpunkti läbiva telje

3. Tasapinnaline paralleelne liikumine

Sissejuhatus analüütilisse mehaanikasse

Analüütilise mehaanika põhimõisted

Analüütiline mehaanika- mehaanika valdkond (lõik), kus mehaaniliste süsteemide liikumist või tasakaalu uuritakse üldiste, ühtsete analüütiliste meetodite abil, mida kasutatakse mis tahes mehaaniliste süsteemide puhul.

Vaatleme analüütilise mehaanika kõige iseloomulikumaid mõisteid.

1. Ühendused ja nende klassifikatsioon.

Ühendused– mehaanilise süsteemi punktide liikumisele kehtestatud mis tahes piirangud kehade kujul või mis tahes kinemaatilisi tingimusi. Neid piiranguid saab kirjutada võrrandite või võrratustena.

Geomeetrilised ühendused-- ühendused, mille võrrandid sisaldavad ainult punktide koordinaate, st piirangud on seatud ainult punktide koordinaatidele. Need on ühendused kehade, pindade, joonte jne kujul.

Diferentsiaalühendused-- ühendused, mis seavad piiranguid mitte ainult punktide koordinaatidele, vaid ka nende kiirusele.

Holonoomilised ühendused -- kõik geomeetrilised ühendused ja need diferentsiaalühendused, mille võrrandeid saab integreerida.

Mitteholoonsed ühendused-- diferentsiaalsed mitteintegreeritavad ühendused.

Lauaühendused --ühendused, mille võrrandid ei sisalda selgesõnaliselt aega.

Mittestatsionaarne side-- seosed, mis ajas muutuvad, st mille võrrandid sisaldavad selgelt aega.

Kahesuunalised (hoidvad) ühendused --ühendused, mis piiravad punkti liikumist kahes vastassuunas. Selliseid seoseid kirjeldavad võrrandid .

Ühepoolne(mittepidurdavad) ühendused - ühendused, mis piiravad liikumist ainult ühes suunas. Selliseid seoseid kirjeldavad ebavõrdsused

2. Võimalikud (virtuaalsed) ja tegelikud liikumised.

Võimalik või virtuaalne mehaanilise süsteemi punktide nihked on kujuteldavad lõpmata väikesed liikumised, mis võimaldavad süsteemile peale surutud seoseid.

Võimalik Mehaanilise süsteemi liikumine on süsteemi punktide samaaegsete võimalike liikumiste kogum, mis ühilduvad ühendustega. Olgu mehaaniline süsteem vändamehhanism.

Punkti võimalik liikumine A on liikumine, mida oma väiksuse tõttu peetakse sirgjooneliseks ja mis on suunatud sellega risti OA.

Punkti võimalik liikumine IN(liugur) liigub juhikutes. Vända võimalik liikumine OA on pöördenurk ja ühendusvarras AB -- nurga all ümber MCS-i (punkt R).

Kehtiv süsteemi punktide nihkeid nimetatakse ka elementaarnihketeks, mis võimaldavad üksteise peale asetatud seoseid, kuid arvestades liikumise algtingimusi ja süsteemile mõjuvaid jõude.

Kraadide arv vabadust S Mehaaniline süsteem on selle sõltumatute võimalike liikumiste arv, mida saab kindlal ajahetkel süsteemi punktidele edastada.

Võimalike liikumiste põhimõte (Lagrange'i põhimõte)

Võimalike nihete printsiip ehk Lagrange’i printsiip väljendab mittevaba mehaanilise süsteemi tasakaaluseisundit rakendatud aktiivjõudude mõjul. Põhimõtte avaldus.

Tasakaaluks Kahesuunaliste, statsionaarsete, holonoomiliste ja ideaalühendustega mittevaba mehaanilise süsteemi puhul, mis on rakendatud aktiivjõudude toimel puhkeasendis, on vajalik ja piisav, et kõigi aktiivjõudude elementaartööde summa on võrdne täpp süsteemi võimaliku nihke kohta vaadeldavast tasakaaluasendist:

Dünaamika üldvõrrand (Lagrange-D'Alemberti põhimõte)

Dünaamika üldvõrrandit rakendatakse mittevabade mehaaniliste süsteemide liikumise uurimisel, mille kehad või punktid liiguvad teatud kiirendustega.

Vastavalt d'Alemberti põhimõttele moodustab mehaanilisele süsteemile rakendatud aktiivsete jõudude kogum, mis ühendab reaktsioonijõude ja inertsjõude süsteemi kõigis punktides, tasakaalustatud jõudude süsteemi.

Kui rakendada sellisele süsteemile võimalike nihkete põhimõtet (Lagrange’i põhimõte), saame kombineeritud Lagrange-D’Alemberti printsiibi või dünaamika üldvõrrand.Selle põhimõtte avaldus.

Vabalt liikumisel Kahesuunalise, ideaalse, statsionaarse ja holonoomilise ühendusega mehaanilise süsteemi puhul on süsteemi mis tahes võimaliku liikumise korral süsteemi punktidele rakenduvate kõigi aktiivjõudude ja inertsjõudude elementaartööde summa null:

Teist tüüpi Lagrange'i võrrandid

Lagrange'i võrrandid teist tüüpi on mehaanilise süsteemi liikumise diferentsiaalvõrrandid üldistatud koordinaatides.

Süsteemi jaoks, millel on S vabadusastmete puhul on neil võrranditel vorm

Erinevus süsteemi kineetilise energia osatuletise ajaline summaarne tuletis üldistatud kiiruse suhtes ja kineetilise energia osatuletis üldistatud koordinaadi suhtes on võrdne üldistatud jõuga.

Lagrange'i võrrandid konservatiivsete mehaaniliste süsteemide jaoks. Tsüklilised koordinaadid ja integraalid

Konservatiivse süsteemi korral määratakse üldistatud jõud süsteemi potentsiaalse energia kaudu valemi järgi

Seejärel kirjutatakse Lagrange'i võrrandid kujul ümber

Kuna süsteemi potentsiaalne energia on ainult üldistatud koordinaatide funktsioon, siis seda arvesse võttes esitagem see kujul, kus T - P = L -- Lagrange'i funktsioon (kineetiline potentsiaal). Lõpuks Lagrange'i võrrandid konservatiivse süsteemi jaoks

Mehaanilise süsteemi tasakaaluasendi stabiilsus

Mehaaniliste süsteemide tasakaaluasendi stabiilsuse küsimus on süsteemide vibratsiooniteoorias otsese tähtsusega.

Tasakaaluasend võib olla stabiilne, ebastabiilne ja ükskõikne.

Säästev tasakaaluasend - tasakaaluasend, milles mehaanilise süsteemi punktid, mis on sellest asendist eemaldatud, liiguvad seejärel jõudude toimel nende tasakaaluasendi vahetus läheduses.

Sellel liigutusel on teatud ajaline korratavus, st süsteem sooritab võnkuva liikumise.

Ebastabiilne tasakaaluasend - tasakaaluasend, millest süsteemi punktide suvaliselt väikese kõrvalekalde korral viivad edasised jõud punktid nende tasakaaluasendist veelgi kaugemale. .

Ükskõikne tasakaaluasend - tasakaaluasend, kui süsteemi punktide mis tahes väikese alghälbe korral sellest asendist jääb süsteem uues asendis samuti tasakaalu. .

Mehaanilise süsteemi stabiilse tasakaaluasendi määramiseks on erinevaid meetodeid.

Vaatleme stabiilse tasakaalupositsiooni määratlust, mis põhineb Lagrange-Dirichlet' teoreemid

Kui asendis ideaalsete ja statsionaarsete ühendustega konservatiivse mehaanilise süsteemi tasakaal, selle potentsiaalne energia on miinimumiga, siis on see tasakaaluasend stabiilne.

Mõju nähtus. Löögijõud ja löögiimpulss

Nähtust, kus keha punktide kiirused muutuvad ebaoluliselt väikese aja jooksul lõplikult, nimetatakse löök. Seda ajaperioodi nimetatakse mõju aeg. Löögi ajal avaldatakse löögijõudu lõpmata lühikese aja jooksul. Löögi jõud nimetatakse jõuks, mille impulss löögi ajal on lõplik väärtus.

Kui jõud on moodulis lõplik tegutseb aja jooksul, alustades oma tegevust ajahetkel , siis on selle impulsil vorm

Kui löögijõud mõjub materiaalsele punktile, võime öelda, et:

mittehetkeliste jõudude mõju löögi ajal võib tähelepanuta jätta;

materiaalse punkti liikumist löögi ajal võib ignoreerida;

löögijõu mõju materiaalsele punktile väljendub selle kiirusvektori lõplikus muutuses löögi ajal.

Teoreem mehaanilise süsteemi impulsi muutumise kohta kokkupõrkel

mehaanilise süsteemi impulsi muutus kokkupõrke ajal võrdub kõigi süsteemide punktidele rakendatud väliste löögiimpulsside geomeetrilise summaga, Kus - mehaanilise süsteemi liikumise suurus löögijõudude lõppemise hetkel, - mehaanilise süsteemi liikumise suurus hetkel, mil löögijõud hakkavad mõjuma, - väline šokiimpulss.

D'Alemberti põhimõte kehtestab ühtse lähenemise materiaalse objekti liikumise uurimisele, olenemata sellele liikumisele seatud tingimuste olemusest. Sel juhul antakse dünaamilised liikumisvõrrandid tasakaaluvõrrandite kujul. Sellest ka d'Alemberti printsiibi teine ​​nimetus – kinetostaatiline meetod.

Materiaalse punkti mis tahes liikumishetkel on rakendatud aktiivjõudude, sidestusreaktsioonide ja tavapäraselt seotud inertsjõu geomeetriline summa võrdne nulliga (joonis 48).

kus F on materiaalse punkti inertsjõud, mis on võrdne:

. (15.2)

Joonis 48

Joonis 49

Inertsjõud ei rakendu mitte liikuvale objektile, vaid seostele, mis määravad selle liikumise. Mees teatab kiirendusest käru (joon. 49), surudes seda jõuga .Inertsjõud kujutab endast vastumõju kärul oleva inimese tegevusele, s.t. moodul võrdne jõuga ja suunatud vastupidises suunas.

Kui punkt liigub mööda kõverat rada, siis saab inertsjõu projitseerida loomulikele koordinaatide telgedele.

Joonis 50

; (15.3)

, (15.4) kus -- trajektoori kõverusraadius.

Probleemide lahendamisel kinetostaatika meetodi abil peate:

1. vali koordinaatsüsteem;

2. näidata kõiki igale punktile rakenduvaid aktiivjõude;

3. visake ühendused ära, asendades need sobivate reaktsioonidega;

4. liita seoste aktiivjõududele ja reaktsioonidele inertsjõud;

5. koostada kinetostaatilisi võrrandeid, mille põhjal määrata vajalikud suurused.

NÄIDE 21.

KOHTA

LAHENDUS.

1. Vaatleme autot, mis asub kumera silla ülemises punktis. Vaatleme autot kui materiaalset punkti, millel on antud jõud ja suhtlusreaktsioon .

2. Kuna auto liigub konstantsel kiirusel, siis kirjutame D’Alemberti põhimõtte normaalsele projektsioonis oleva materiaalse punkti jaoks üles
. (1) Avaldame inertsjõudu:
; Auto normaalrõhu määrame võrrandist (1): N.

määrata raadiusega kumera silla ülemises punktis G=10000H kaaluva auto rõhk =20m ja liikudes püsiva kiirusega V=36km/h (joon. 51).

16. D'Alemberti põhimõte mehaanilise süsteemi jaoks. Inertsjõudude põhivektor ja põhimoment.

Kui mehaanilise süsteemi igale punktile rakendatakse tinglikult vastav inertsiaaljõud igal liikumishetkel, siis igal liikumishetkel on punktile mõjuvate aktiivjõudude, ühenduste reaktsioonide ja inertsijõu geomeetriline summa võrdne null.

Võrrandil, mis väljendab d'Alemberti põhimõtet mehaanilise süsteemi jaoks, on vorm
. (16.1) Nende tasakaalustatud jõudude momentide summa mis tahes tsentri suhtes on samuti null
. (16.2) D'Alemberti printsiibi rakendamisel koostatakse süsteemi liikumisvõrrandid tasakaaluvõrranditena. Kasutades võrrandeid (16.1) ja (16.2), saab määrata dünaamilisi reaktsioone.

NÄIDE 22.

Vertikaalne AK-võll, mis pöörleb konstantse nurkkiirusega =10s -1, mis on kinnitatud tõukelaagriga punktis A ja silindrilise laagriga punktis K (joonis 52). Võlli külge punktis E on kinnitatud õhuke homogeenne murtud varras massiga m = 10 kg ja pikkusega 10 b, mis koosneb osadest 1 ja 2, kus b = 0,1 m ning nende massid m 1 ja m 2 on võrdeline pikkustega. Varras on võlli külge kinnitatud hingega punktis E ja kaaluta vardaga 4, mis on jäigalt kinnitatud punktis B. Määrake hinge E ja varda 4 reaktsioon.

LAHENDUS.

1. Katkise varda pikkus on 10b. Avaldame varda osade massid võrdeliselt pikkustega: m 1 =0,4m; m2 = 0,3 m; m 3 =0,3 m.

Joonis 42

2. Soovitud reaktsioonide kindlaksmääramiseks kaaluge purunenud varda liikumist ja rakendage D’Alemberti põhimõtet. Asetame varda xy tasapinnale ja kujutame sellele mõjuvaid välisjõude: ,,, hinge reaktsioonid Ja ja reaktsioon
varras 4. Nendele jõududele liidame varda osade inertsijõud:
;
;
,

Kus
;
;
.

Siis N.N.N.

Resultantsete inertsijõudude toimejoon ,
Ja
läbib kaugustel h 1, h 2 ja h 3 x teljest: m;

3. D'Alemberti põhimõtte kohaselt moodustavad rakendatud aktiivjõud, sidestusreaktsioonid ja inertsiaaljõud tasakaalustatud jõudude süsteemi. Koostame tasapinnalise jõudude süsteemi jaoks kolm tasakaaluvõrrandit:

; ; (1)
;; (2)
;.(3)

Lahendades võrrandisüsteemi (1)+(3), asendades vastavate suuruste antud väärtused, leiame vajalikud reaktsioonid:

N= y E = x E =

Kui kõik mehaanilise süsteemi punktidele mõjuvad jõud jagada välisteks ja sisemine , (joonis 53), siis mehaanilise süsteemi suvalise punkti jaoks võime kirjutada kaks vektorvõrdsust:

; (16.3)
.

Joonis 53

Võttes arvesse sisejõudude omadusi, saame d'Alemberti põhimõtte mehaanilise süsteemi jaoks järgmisel kujul:
; (16.4)
, (16.5) kus ,-- vastavalt välisjõudude ja inertsiaalsete jõudude põhivektorid;

,
-- vastavalt välisjõudude ja inertsjõudude peamised momendid suvalise keskpunkti O suhtes.

Peavektor ja põhipunkt
asendada süsteemi kõigi punktide inertsiaaljõud, kuna süsteemi igal punktil peab olema oma inertsiaaljõud, mis sõltub punkti kiirendusest. Kasutades teoreemi massikeskme liikumise ja süsteemi nurkimpulsi muutumise kohta suvalise keskpunkti suhtes, saame:
, (16.6)

. (16.7) Ümber fikseeritud telje z pöörleva jäiga keha puhul on selle telje suhtes tekkivate jõudude peamine inertsmoment võrdne
, (16.8) kus -- keha nurkkiirendus.

Keha translatsioonilise liikumise ajal taandatakse kõigi selle punktide inertsiaaljõud resultandiks, mis on võrdne inertsijõudude peavektoriga, s.o.
.

P

Joonis 54

Kui keha pöörleb ümber massikeskpunkti läbiva fikseeritud telje z, taandatakse keha kõigi punktide inertsiaaljõud jõudude paariks, mis paikneb pöörlemisteljega risti ja millel on moment.
, (16.9) kus -- keha inertsimoment pöörlemistelje suhtes.

Kui kehal on sümmeetriatasapind ja see pöörleb ümber fikseeritud telje z, mis on sümmeetriatasandiga risti ja ei läbi keha massikeset, taandatakse keha kõigi punktide inertsiaaljõud resultantjõuks, mis on võrdne süsteemi inertsijõudude peavektorile, kuid rakendatud mõnele punktile K (joon. 54) . Tulemuse tegevusliin asub punktist O kaugel
. (16.10)

Sümmeetriatasandiga keha tasapinnalisel liikumisel liigub keha mööda seda tasapinda (joon. 55). Sellel tasapinnal asuvad ka inertsjõudude põhivektor ja põhimoment ning need määratakse valemitega:

Joonis 55

;

.

Miinusmärk näitab hetke suunda
vastupidine keha nurkkiirenduse suunale.

NÄIDE 23.

Määrake jõud, mis kipub rebenema ühtlaselt pöörlevat hooratast massiga m, võttes arvesse selle massi jaotumist üle velje. Hooratta raadius r, nurkkiirus (joonis 56).

LAHENDUS.

1. Jõudu, mida otsid on sisemine. -- velje elementide inertsjõudude resultant.
. Avaldame velje kaare massikeskme koordinaati x c kesknurgaga
:
, Siis
.

2. Tugevuse määramiseks Rakendame d'Alemberti põhimõtet projektsioonis x-teljele:
;
, kus
.

3. Kui hooratas on tahke homogeenne ketas, siis
, Siis
.

d'Alemberti põhimõte kasutatakse mittevaba punkti dünaamika esimese põhiülesande lahendamisel, kui on teada punkti liikumine ja sellele mõjuvad aktiivjõud ning otsitakse sellest tulenevat seose reaktsiooni.

Kirjutame üles mittevaba punkti dünaamika põhivõrrandi inertsiaalses võrdlusraamis:

Kirjutame võrrandi ümber järgmiselt:

.

Tähistades , saame

, (11.27)

kus vektorit kutsutakse D'Alemberti inertsiaaljõud.

Põhimõtte avaldus: Mittevaba materiaalse punkti igal liikumishetkel tasakaalustatakse ühenduse aktiivjõudu ja reaktsiooni D'Alemberti inertsjõuga..

Projekteerides vektorvõrrandi (11.27) mis tahes koordinaattelgedele, saame vastavad tasakaaluvõrrandid, mille abil saame leida tundmatuid reaktsioone.

Projekteerime võrrandi (11.27) loomulikele telgedele:

(11.28)

Kus nimetatakse inertsi tsentrifugaaljõuks, mis on alati suunatud põhinormaali negatiivses suunas; .

Märkused:

1). Tegelikkuses lisaks jõududele punktile muid füüsilisi jõude ei rakendata ja need kolm jõudu ei moodusta tasakaalustatud jõudude süsteemi. Selles mõttes on d'Alemberti inertsiaaljõud fiktiivne jõud, mis on punktile tinglikult rakendatud.

2). D'Alemberti põhimõtet tuleks käsitleda kui mugavat metoodilist vahendit, mis võimaldab dünaamika probleemi taandada staatika probleemiks.

Näide 1. Määrakem piloodile mõjuv sidestusreaktsioon vertikaaltasandil liikuva õhusõiduki sukeldumislennult väljumisel (joonis 11.5).

Pilooti mõjutab gravitatsioon ja istme reaktsioon. Rakendame D'Alemberti põhimõtet, lisades neile jõududele D'Alemberti inertsjõu:

(11.29)

Kirjutame võrrandi (11.29) projektsioonidesse normaalsele:

(11.30)

Kus r- ringi raadius, kui õhusõiduk siseneb tasapinnale,

Lennuki maksimaalne kiirus antud hetkel.

Võrrandist (11.30)

(11.31)

Näide 2. Määrame nüüd sama reaktsiooni, mis mõjub piloodile tõusurežiimist väljumise hetkel (joonis 11.6).

Materiaalse punkti suhteline liikumine

Kui tugisüsteemid ei liigu translatsiooniliselt inertsiaalse võrdlussüsteemi suhtes või nende koordinaatide alguspunktid liiguvad ebaühtlaselt või kõverjooneliselt, siis on sellised referentssüsteemid mitteinertsiaalne. Nendes võrdlusraamides on aksioomid A 1 ja A 2 ei vaadelda, kuid sellest ei järeldu, et dünaamikas uuritakse ainult inertsiaalsetes referentssüsteemides toimuvaid liikumisi. Vaatleme materiaalse punkti liikumist mitteinertsiaalses koordinaatsüsteemis, kui on teada materiaalsele punktile mõjuvad jõud ja on määratud mitteinertsiaalse tugisüsteemi liikumine inertsiaalse tugisüsteemi suhtes. Järgnevalt nimetatakse inertsiaalset tugiraamistikku statsionaarseks ja mitteinertsiaalset tugiraamistikku liikuvaks tugiraamiks. Laskma olema punktile mõjuvate aktiivsete jõudude resultant ja olema sidemete reaktsiooni resultant; - fikseeritud koordinaatsüsteem; - liikuv koordinaatsüsteem.

Mõelge materiaalse punkti liikumisele M(joon. 11.7), mis pole liikuva koordinaatsüsteemiga jäigalt seotud, vaid liigub selle suhtes. Kinemaatikas nimetati seda punkti liikumist suhteliseks, punkti liikumist fikseeritud koordinaatsüsteemi suhtes absoluutseks ja liikuva koordinaatsüsteemi liikumist portatiivseks.

Punkti absoluutse liikumise dünaamika põhiseadus M hakkab välja nägema

(11.33)

kus on punkti absoluutne kiirendus.

Lähtudes kinemaatika kiirenduste liitmise teoreemist (Coriolise teoreem), on absoluutne kiirendus suhteliste, transpordi- ja Coriolise kiirenduste summa.

. (11.34)

Asendades (11.34) väärtusega (11.33), saame

ja pärast tähiste ülekandmist ja sisestamist

(11.35)

Kus; vektorit nimetatakse inertsi ülekandejõuks; - Coriolise inertsjõud.

Võrdsus (11.35) väljendab punkti suhtelise liikumise seadust. Järelikult võib punkti liikumist mitteinertsiaalses võrdlusraamis pidada liikumiseks inertsiaalses raamis, kui liidame punktile mõjuvate aktiivjõudude ja sidestusreaktsioonide arvule ülekande- ja Coriolise inertsiaaljõud.

Kõik dünaamikaprobleemide lahendamise meetodid, mida oleme seni käsitlenud, põhinevad võrranditel, mis tulenevad kas otse Newtoni seadustest või üldistest teoreemidest, mis on nende seaduste tagajärjed. See tee pole aga ainus. Selgub, et mehaanilise süsteemi liikumisvõrrandid või tasakaalutingimused on võimalik saada, kui lähtuda Newtoni seaduste asemel muudest üldpõhimõtetest, mida nimetatakse mehaanika põhimõteteks. Paljudel juhtudel võimaldab nende põhimõtete rakendamine, nagu näeme, leida tõhusamaid meetodeid vastavate probleemide lahendamiseks. Selles peatükis vaadeldakse üht mehaanika üldpõhimõtet, mida nimetatakse d'Alemberti põhimõtteks.

Olgu meil süsteem, mis koosneb n materiaalsed punktid. Valime ühe massiga süsteemi punktidest. Sellele rakendatavate välis- ja sisejõudude (mis hõlmavad nii aktiivseid jõude kui ka sidestusreaktsioone) mõjul saab punkt inertsiaalse võrdlusraami suhtes mõningase kiirenduse.

Võtkem arvesse kogust

millel on jõu mõõde. Vektorsuurust, mille suurus on võrdne punkti massi ja selle kiirenduse korrutisega ning mis on suunatud sellele kiirendusele vastupidi, nimetatakse punkti inertsiaaljõuks (mõnikord ka d’Alemberti inertsiaaljõuks).

Siis selgub, et punkti liikumisel on järgmine üldomadus: kui igal ajahetkel lisada punktile tegelikult mõjuvatele jõududele inertsjõud, siis tekib tekkinud jõudude süsteem tasakaalus, s.t. tahe

.

See väljend väljendab d'Alemberti põhimõtet ühe materiaalse punkti kohta. On lihtne näha, et see on samaväärne Newtoni teise seadusega ja vastupidi. Tegelikult annab Newtoni teine ​​seadus kõnealuse punkti kohta . Liigutades terminit siin võrdsuse paremale poolele, jõuame viimase seoseni.

Korrates ülaltoodud arutluskäiku seoses süsteemi iga punktiga, jõuame järgmise tulemuseni, mis väljendab süsteemi jaoks D'Alemberti põhimõtet: kui igal ajahetkel rakendatakse süsteemi igale punktile lisaks sellele tegelikult mõjuvatele välis- ja sisejõududele vastavad inertsiaalsed jõud, siis on tulemuseks olev jõudude süsteem tasakaalus ja kõik staatilised võrrandid on sellele rakendatud.

D'Alemberti printsiibi olulisus seisneb selles, et dünaamika probleemidele vahetult rakendatuna koostatakse süsteemi liikumisvõrrandid hästituntud tasakaaluvõrrandite kujul; mis teeb probleemide lahendamisel ühtse lähenemise ja tavaliselt lihtsustab oluliselt vastavaid arvutusi. Lisaks võimaldab d'Alemberti põhimõte koos võimalike nihkete põhimõttega, millest tuleb juttu järgmises peatükis, saada uue üldmeetodi dünaamikaülesannete lahendamiseks.

D'Alembert' printsiibi rakendamisel tuleb meeles pidada, et mehaanilise süsteemi punktile, mille liikumist uuritakse, mõjutavad ainult välised ja sisemised jõud ning , mis tekivad süsteemi punktide vastasmõju tulemusena. süsteem omavahel ja süsteemi mittekuuluvate kehadega; nende jõudude mõjul liiguvad süsteemi punktid vastavate kiirendustega. Inertsijõud, millest on juttu D'Alemberti printsiibist, ei mõju liikuvatele punktidele (muidu oleksid need punktid paigal või liiguksid ilma kiirenduseta ja siis poleks inertsijõude ennast). Inertsiaalsete jõudude kasutuselevõtt on lihtsalt tehnika, mis võimaldab koostada dünaamilisi võrrandeid, kasutades lihtsamaid staatilisi meetodeid.

Staatikast on teada, et tasakaalus olevate jõudude geomeetriline summa ja nende momentide summa mis tahes keskpunkti suhtes KOHTA on võrdsed nulliga ja tahkumise põhimõtte kohaselt kehtib see mitte ainult tahkele kehale, vaid ka mis tahes muutuvale süsteemile mõjuvate jõudude kohta. Siis peaks D'Alemberti põhimõttest lähtudes olema.