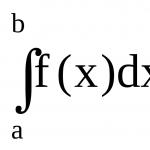Pindala arvutamine kindla integraali abil. Etteantud joontega piiratud kujundite pindalade arvutamine. IV. Uue materjali selgitus
Definitsioonist järeldub, et mittenegatiivse funktsiooni f(x) korral on kindel integraal võrdne kõverjoonelise trapetsi pindalaga, mis on piiratud kõveraga y = f(x), sirgjooned x = a, x = b ja abstsiss = 0 (joonis 4.1).
Kui funktsioon – f(x) on mittepositiivne, siis on kindel integraal 
võrdne vastava kõverjoonelise trapetsi pindalaga, mis on võetud miinusmärgiga (joonis 4.7).
Joonis 4.7 – Mittepositiivse funktsiooni kindla integraali geomeetriline tähendus
Suvalise pideva funktsiooni f(x) korral on kindel integraal 
on võrdne funktsiooni f(x) graafiku all ja abstsissteljest kõrgemal asuvate kõverjooneliste trapetside pindalade summaga, millest on lahutatud funktsiooni f(x) graafiku kohal ja allpool olevate kõverjooneliste trapetside pindalade summa. abstsisstelg (joonis 4.8).
Joonis 4.8 – Suvalise pideva funktsiooni f(x) kindla integraali geomeetriline tähendus (pluss märgib liidetavat ala, miinus aga lahutatavat ala).
Praktikas kasutatakse kõverjoonte pindalade arvutamisel sageli järgmist valemit: 
, kus S on lõigu [a,b] kõverate y = f 1 (x) ja y = f 2 (x) ning f 1 (x) ja f 2 (x) vahele jääva joonise pindala ) on sellel lõigul defineeritud pidevad funktsioonid, nii et f 1 (x) ≥ f 2 (x) (vt joonised 4.9, 4.10).
Tuletise majanduslikku tähendust uurides selgus, et tuletis toimib mõne majandusobjekti või protsessi muutumise kiirusena ajas või mõne muu uuritava teguri suhtes. Teatud integraali majandusliku tähenduse kindlakstegemiseks on vaja seda kiirust ennast pidada aja või muu teguri funktsiooniks. Siis, kuna kindel integraal tähistab muutust antiderivatiivis, saame, et majandusteaduses hindab ta selle objekti (protsessi) muutust teatud ajaperioodi jooksul (või mõne muu teguri teatud muutusega).
Näiteks kui funktsioon q=q(t) kirjeldab tööviljakust sõltuvalt ajast, siis selle funktsiooni kindel integraal 
tähistab väljundi Q mahtu ajavahemikul t 0 kuni t 1.
Kindlate integraalide arvutamise meetodid põhinevad varem käsitletud integreerimismeetoditel (me ei teosta tõestusi).
Määramata integraali leidmisel kasutasime muutuja muutmise meetodit valemi alusel: f(x)dx= =f((t))`(t)dt, kus x =(t) on funktsioon vaadeldava vahel eristatav. Kindla integraali korral võtab muutuja muutumise valem kuju 
, Kus 
ja kõigile.
Näide 1. Otsi
Olgu t= 2 – x 2. Siis dt = -2xdx ja xdx = - ½ dt.
Kui x = 0 t= 2 – 0 2 = 2. Kui x = 1t= 2 – 1 2 = 1. Siis
Näide 2. Otsi
Näide 3. Otsi
Osade kaupa integreerimise valem kindla integraali jaoks on järgmine: 
, Kus 
.
Näide 1. Otsi
Olgu u=ln(1 +x),dv=dx. Siis
Näide 2. Otsi
Tasapinnaliste kujundite pindalade arvutamine kindla integraali abil
Näide 1. Leidke joonise pindala, mis on piiratud joontega y = x 2 – 2 ja y = x.
Funktsiooni y= x 2 – 2 graafik on parabool, mille miinimumpunkt on x= 0, y= -2; Abstsisstelg lõikub punktides 
. Funktsiooni y = x graafik on sirge, mittenegatiivse koordinaatkvadrandi poolitaja.
Leiame parabooli y = x 2 – 2 ja sirge y = x lõikepunktide koordinaadid, lahendades nende võrrandite süsteemi:
x 2 – x – 2 = 0
x = 2; y = 2 või x = -1;y = -1
Seega saab joonisel 4.9 kujutada joonist, mille pindala on vaja leida.
Joonis 4.9 – joontega y = x 2 – 2 ja y = x piiratud joonis
Lõigul [-1, 2] x ≥ x 2 – 2.
Kasutame valemit 
, pannes f 1 (x) = x; f 2 (x) = x 2 – 2;a= -1;b= 2.
Näide 2. Leidke joonise pindala, mis on piiratud joontega y = 4 - x 2 ja y = x 2 - 2x.
Funktsiooni y = 4 - x 2 graafik on parabool, mille maksimaalne punkt on x = 0, y = 4; X-telg lõikub punktides 2 ja -2. Funktsiooni y = x 2 – 2x graafik on parabool, mille miinimumpunkt on 2x- 2 = 0, x = 1, y = -1; X-telg lõikub punktides 0 ja 2.
Leiame kõverate lõikepunktide koordinaadid:
4 - x 2 = x 2 - 2x
2x 2 - 2x - 4 = 0
x 2 – x – 2 = 0
x = 2; y = 0 või x = -1;y = 3
Seega saab joonisel 4.10 kujutada joonist, mille pindala on vaja leida.
Joonis 4.10 – joontega y = 4 - x 2 ja y = x 2 - 2x piiratud joonis
Lõigul [-1, 2] 4 - x 2 ≥ x 2 - 2x.
Kasutame valemit 
, pannes f 1 (x) = 4 - - x 2; f 2 (x) = x 2 – 2x;a= -1;b= 2.
Näide 3. Leidke mittenegatiivses koordinaatkvadrandis joontega y = 1/x; y= x 2 ja y= 4 piiratud joonise pindala.
Funktsiooni y = 1/x graafik on hüperbool, positiivse x korral on see allapoole kumer; koordinaatteljed on asümptoodid. Funktsiooni y = x 2 graafik mittenegatiivses koordinaatkvadrandis on parabooli haru, mille lähtepunktis on minimaalne punkt. Need graafikud ristuvad punktis 1/x = x 2; x 3 = 1; x = 1; y = 1.
Funktsiooni y = 1/x graafik lõikab sirget y = 4 punktis x = 1/4 ja funktsiooni y = x 2 graafikut punktis x = 2 (või -2).
Seega saab joonisel 4.11 kujutada joonist, mille pindala on vaja leida.
Joonis 4.11 – joontega y = 1/x piiratud joonis; y= x 2 ja y= 4 mittenegatiivses koordinaatkvadrandis
Joonise ABC nõutav pindala on võrdne ristküliku ABHE pindala, mis on võrdne 4*(2 – ¼) = 7, ja kahe kõverjoonelise trapetsi ACFE ja pindalade summa vahega. CBHF. Arvutame ACFE pindala:
Arvutame pindala SVНF:
.
Seega on nõutav pindala 7 – (ln4 + 7/3) = 14/3 –ln43,28 (ühik 2).
Matemaatikatund keskkutseõppeasutuste I kursusele
Teema: "Tasapindade pindalade arvutamine kindla integraali abil."
Matemaatikaõpetaja S.B. Baranova
Hariduslikud eesmärgid:
tagada selleteemalise materjali kordamine, üldistamine ja süstematiseerimine;
luua tingimused teadmiste ja oskuste kontrollimiseks (enesekontrolliks).
Arendusülesanded:
edendada võrdlemise, üldistamise ja peamise esiletõstmise tehnikate rakendamise oskuste kujunemist;
jätkata matemaatilise silmaringi, mõtlemise ja kõne, tähelepanu ja mälu arendamist.
Õppeülesanded:
edendada huvi matemaatika vastu;
aktiivsus-, liikuvus-, suhtlemisoskuste harimine.
Tunni tüüp – kombineeritud tund probleemõppe elementidega.
Õppemeetodid ja tehnikad – problemaatiline, visuaalne, õpilaste iseseisev töö, enesekontroll.
Varustus – tunni lisa, tabelid.
Tunniplaan
Aja organiseerimine. Õpilaste ettevalmistamine tööks tunnis.
Õpilaste ettevalmistamine aktiivseks tööks (arvutusoskuste ja integraalitabelite testimine rühmade kaupa).
Ettevalmistus uue materjali õppimiseks läbi kordamise ja algteadmiste uuendamise.
Töö uue materjaliga.
Õpitava materjali esmane mõistmine ja rakendamine, selle kinnistamine.
Kodutöö.
Teadmiste rakendamine.
Kokkuvõtteid tehes.
Peegeldus.
Tundide ajal
1. Organisatsioonimoment.
Määratletud integraali mõiste on matemaatika üks põhimõisteid. 17. sajandi lõpuks. Newton ja Leibniz lõid diferentsiaal- ja integraalarvutuse aparaadi, mis on matemaatilise analüüsi aluseks.
Eelmistes tundides õppisime määramatuid integraale “võtma” ja kindlaid integraale arvutama. Kuid palju olulisem on kindla integraali kasutamine. Teame, et seda saab kasutada kõverate trapetside pindalade arvutamiseks. Täna vastame küsimusele: "Kuidas seda teha?"
2. Õpilaste ettevalmistamine aktiivseks tööks.
Kuid kõigepealt peame proovile panema oma arvutusoskused ja integraalitabeli tundmise. Enne sind on ülesanne, mille tulemuseks on prantsuse matemaatiku S.D. Poisson (Elu rikastavad kaks asja: matemaatikaga tegelemine ja selle õpetamine).
Ülesanne sooritatakse paarikaupa ().
3. Ettevalmistus uue materjali õppimiseks läbi kordamise ja algteadmiste täiendamise.
Liigume edasi meie tunni teema juurde: “Tasapinnakujude pindalade arvutamine kindla integraali abil”. Lisaks kindla integraali arvutamise võimalusele peame meeles pidama alade omadusi. Mis need on?
Võrdsetel arvudel on võrdsed alad.
Kui kujund on jagatud kaheks osaks, siis leitakse selle pindala üksikute osade pindalade summana.
Samuti peame kordama integraalsumma reeglit ja Newtoni-Leibnizi valemit.
4. Uue integraaliga töötamine
1. Määratud integraali kasutatakse kõverjooneliste trapetside pindalade arvutamiseks. Kuid praktikas on sagedamini kujundeid, mis pole sellised, ja me peame õppima, kuidas leida just selliste kujundite pindala.
Töötage tabeli “Tasapinnalise kujundi paigutuse põhijuhud ja vastavad pindalavalemid” järgi ().
2. Paneme end proovile.
Töötage ülesandega (), millele järgneb kontrollimine (tabel nr 3).
3. Kuid oskusest valida ala jaoks õiged valemid ei piisa. Järgmises tabelis () on igas ülesandes "väline" põhjus, mis ei võimalda joonise pindala arvutamist. Otsime nad üles.
a) funktsioonide graafikute valemeid pole näidatud.
b) integratsioonil pole piire.
c) graafikute nimetusi pole märgitud ja ühest piirangut pole.
d) ühe graafiku valemit pole näidatud.
4. Arvestades tehtud töid, sõnastame ja paneme kirja tunni teemal ülesannete lahendamise algoritmi.
Koostage nendest joontest graafikud. Määrake soovitud näitaja.
Leidke integratsiooni piirid.
Kirjutage soovitud joonise pindala kindla integraali abil.
Arvutage saadud integraal.
5. Õpitava materjali esmane mõistmine ja rakendamine, selle kinnistamine.
1. Võttes arvesse algoritmi, täidame viimase tabeli ülesande nr 2.
1. pilt
Lahendus:
Punkti A jaoks:
– ei vasta ülesande tingimustele
Punkti B jaoks:
– ei vasta probleemi tingimustele.
Vastus: (ruutühikut).
2. Kuid selle ülesande täitmisel ei rakendatud algoritmi täielikult. Selle väljatöötamiseks täidame järgmise ülesande:
Harjutus. Leidke joontega piiratud kujundi pindala , .
Joonis 2
Lahendus:
– parabool, tipp (m,n).
(0;2) – ülemine
Leiame lõimumise piirid.
Vastus: (ruutühikut).
6. Kodutöö.
Arvutage joontega piiratud kujundi pindala (võtke ülesanne lahti).
7. Teadmiste rakendamine.
Iseseisev töö (lisa nr 5))
8. Kokkuvõtete tegemine.
õppis koostama valemeid tasapinnaliste kujundite pindalade leidmiseks;
leida lõimumise piirid;
arvutage kujundite pindala.
9. Peegeldus.
Õpilastele jagatakse lendlehti. Nad peavad oma tööd hindama, valides ühe etteantud vastusevariandist.
Hinnake tunni raskusastet.
Klassis oli teil:
kergesti;
tavaliselt;
raske.
Olen sellest täielikult aru saanud ja saan seda rakendada;
Olen selle täielikult omandanud, kuid mul on seda raske kasutada;
õppinud osaliselt;
ei saanud aru.
Pärast vastustega tutvumist tehke järeldus õpilaste valmisoleku kohta praktiliseks tööks.
Kasutatud raamatud:
Valutse I.I., Diligulin G.D. Matemaatika tehnikakoolidele.
Kramer N.Sh., Putko B.A., Trishin I.M. Kõrgem matemaatika majandusteadlastele.
Danko P.E., Popov A.G. Kõrgmatemaatika, 1. osa.
Zvanich L.I., Rjazanovski A.R. M., Uus kool.
Ajaleht “Matemaatika”. Kirjastus “Esimene september”.
Lisa nr 1
Arvutage kindlad integraalid ja tunnete ära ühe prantsuse matemaatiku S.D. Poissoni väite.
9
Elu
Kolm
Kaks
Asjad
Amet
Matemaatika
Aritmeetika
Õpetamine
Tema
Kaunistatud
Unustades
Lisa nr 2
LAMEKUGU JA VASTAVATE ALAVALEMITE PÕHIJUHTUMID
______________________________________
_
__________________________________
______
________________________________
______
___________________________________
Joonis, mis on sümmeetriline ordinaattelje või alguspunkti suhtes.
Lisa nr 3
Kasutades kindlat integraali, kirjuta üles valemid joonisel varjutatud kujundite pindalade arvutamiseks.
_________________________________________
__________________________________________
___________________________________________
___________________________________________
____________________________________________
Lisa nr 4
Leidke "väline" põhjus, mis ei võimalda teil joonise pindala arvutada.
1. pilt
Joonis 2
Joonis 3
Joonis 4
_____________________________
Lisa nr 5
Iseseisev töö
valik 1
Kirjutage jooniste pindala integraalide abil ja arvutage need
Joonista kujundid, plmille pindalad on võrdsed järgmiste integraalidega:
Iseseisev töö
2. võimalus
Tehke kindlaks, kas järgmised väited on tõesed:
Salvestage kooskasutades kujundite pindalaintegraale ja arvutada need välja
Joonistage kujundid, mille pindala on võrdne järgmiste integraalidega:
Definitsioon. Erinevust F (b) – F (a) nimetatakse funktsiooni f (x) integraaliks intervallil [ a ; b ] ja seda tähistatakse järgmiselt: = F (b) – F (a) – Newtoni-Leibnizi valem.
Integraali geomeetriline tähendus.
Kõverajoonelise trapetsi pindala, mis on piiratud pideva positiivse graafikuga intervallil [a; b ] funktsioonid f (x), Ox-telg ja read x=a ja x= b:
Pindalade arvutamine integraali abil.
1. Joonise pindala, mis on piiratud pideva negatiivse graafikuga intervallil [a; b ] funktsioonid f (x), Ox-telg ja read x=a ja x= b:
2. Joonise pindala, mis on piiratud pidevate funktsioonide f (x) graafikute ja joontega x=a, x= b:
3. Joonise pindala, mis on piiratud pidevate funktsioonide f (x) graafikutega ja:
4. Joonise pindala, mis on piiratud pidevate funktsioonide f (x) ja Ox-telje graafikutega:
Ülesanded ja testid teemal "Integraal. Pindalade arvutamine integraali abil"
- Integraalne
Tunnid: 4 Ülesanded: 13 Kontrolltööd: 1
- Pindalade arvutamine integraalide abil - Antiderivatiiv ja integraalne hinne 11
Tunnid: 1 Ülesanded: 10 Kontrolltööd: 1
- Antiderivaat - Antiderivatiiv ja integraalne hinne 11
Tunnid: 1 Ülesanded: 11 Kontrolltööd: 1
- Planimeetria: pikkuste ja pindalade arvutamine
Ülesanded: 7
- Arvutused ja teisendused - Ettevalmistus matemaatika ühtseks riigieksamiks matemaatika ühtseks riigieksamiks
Ülesanded: 10
Enne kui hakkate arvutama antud joontega piiratud kujundi pindala, proovige seda kujundit koordinaatsüsteemis kujutada. See muudab probleemi lahendamise palju lihtsamaks.
Selleteemaliste teoreetiliste materjalide õppimine annab teile võimaluse omandada antiderivaati ja integraali mõisted, mõista nendevahelist seost, omandada integraalarvutuse kõige lihtsam tehnika ja õppida integraali rakendama funktsioonide graafikutega piiratud jooniste pindalade arvutamisel. .
Näited.
1. Arvutage integraal
Lahendus:
Vastus: 0.
2. Leidke joontega piiratud joonise pindala
a) f(x) = 2 X – X 2 ja x-telg
Lahendus: Funktsiooni f(x) = 2x - x 2 graafik on parabool. Tipp: (1; 1).
Vastus:(ruutühikut).
Tegelikult pole figuuri pindala leidmiseks vaja nii palju teadmisi määramata ja kindla integraali kohta. Ülesanne “arvuta pindala kindla integraali abil” hõlmab alati joonise koostamist, nii et teie teadmised ja joonistamisoskus on palju pakilisem probleem. Sellega seoses on kasulik värskendada oma mälu põhiliste elementaarfunktsioonide graafikutest ning vähemalt osata konstrueerida sirgjoont ja hüperbooli.
Kõver trapets on lame kujund, mis on piiratud telje, sirgjoonte ja lõigul pideva funktsiooni graafikuga, mis sellel intervallil märki ei muuda. Olgu see kujund asukoht mitte vähem x-telg:
Siis kõverjoonelise trapetsi pindala on arvuliselt võrdne kindla integraaliga. Igal kindlal integraalil (mis eksisteerib) on väga hea geomeetriline tähendus.
Geomeetria seisukohalt on kindel integraal ALA.
See on, teatud integraal (kui see on olemas) vastab geomeetriliselt teatud joonise pindalale. Vaatleme näiteks kindlat integraali. Integrand määrab kõvera telje kohal asuval tasapinnal (soovijad saavad joonistada) ja kindel integraal ise on numbriliselt võrdne vastava kõverjoonelise trapetsi pindalaga.
Näide 1
See on tüüpiline määramisavaldus. Otsuse esimene ja kõige olulisem punkt on joonise konstrueerimine. Veelgi enam, joonis tuleb konstrueerida ÕIGE.
Joonise koostamisel soovitan järgmist järjekorda: Esiteks parem on konstrueerida kõik sirged (kui need on olemas) ja ainult Siis- paraboolid, hüperboolid, muude funktsioonide graafikud. Kasumlikum on koostada funktsioonide graafikuid punkt punktilt.
Selle probleemi puhul võib lahendus välja näha selline.
Joonistame joonise (pange tähele, et võrrand määrab telje):
Segmendil asub funktsiooni graafik telje kohal, Sellepärast:
Vastus:
Pärast ülesande täitmist on alati kasulik vaadata joonist ja aru saada, kas vastus vastab tõele. Sel juhul loendame "silma järgi" joonisel olevate lahtrite arvu - noh, neid on umbes 9, see tundub olevat tõsi. On täiesti selge, et kui saime, ütleme, vastuseks: 20 ruutühikut, siis on ilmselge, et kuskil tehti viga - 20 lahtrit ilmselgelt ei mahu kõnealusele joonisele, kõige rohkem kümmekond. Kui vastus on eitav, siis oli ka ülesanne valesti lahendatud.
Näide 3
Arvutage joonise pindala, mis on piiratud joonte ja koordinaattelgedega.
Lahendus: Teeme joonise:
Kui asub kõver trapets telje all(või vähemalt mitte kõrgem antud telg), siis selle pindala saab leida järgmise valemi abil:
Sel juhul:
Tähelepanu! Neid kahte tüüpi ülesandeid ei tohiks segi ajada:
1) Kui teil palutakse lahendada lihtsalt kindel integraal ilma geomeetrilise tähenduseta, võib see olla negatiivne.
2) Kui teil palutakse leida figuuri pindala kindla integraali abil, siis on pindala alati positiivne! Seetõttu ilmub äsja arutatud valemis miinus.
Praktikas paikneb joonis enamasti nii ülemisel kui alumisel pooltasandil ja seetõttu liigume lihtsamate kooliülesannete juurest edasi sisukamate näidete juurde.
Näide 4
Leidke tasapinnalise kujundi pindala, mis on piiratud joontega , .
Lahendus: Kõigepealt peate joonise lõpetama. Üldiselt huvitab meid pindalaülesannetes joonise konstrueerimisel enim joonte lõikepunktid. Leiame parabooli ja sirge lõikepunktid. Seda saab teha kahel viisil. Esimene meetod on analüütiline. Lahendame võrrandi:
See tähendab, et integratsiooni alumine piir on , integratsiooni ülempiir on .
Võimaluse korral on parem seda meetodit mitte kasutada..
Punkthaaval on sirgeid palju tulusam ja kiirem ehitada ning integratsiooni piirid saavad selgeks "iseenesest". Sellegipoolest tuleb piiride leidmise analüütilist meetodit mõnikord siiski kasutada, kui näiteks graafik on piisavalt suur või detailne konstruktsioon ei toonud esile integreerimise piire (need võivad olla murdosalised või irratsionaalsed). Ja me kaalume ka sellist näidet.
Tuleme tagasi oma ülesande juurde: ratsionaalsem on kõigepealt konstrueerida sirge ja alles siis parabool. Teeme joonise:
Ja nüüd töövalem: Kui segmendil on pidev funktsioon suurem või võrdne mõni pidev funktsioon , siis nende funktsioonide graafikute ja joontega piiritletud joonise pindala , leiate valemiga: 
Siin ei pea te enam mõtlema, kus joonis asub - telje kohal või telje all ja jämedalt öeldes loeb, milline graafik on KÕRGEM(teise graafiku suhtes), ja milline neist on ALL.
Vaadeldavas näites on ilmne, et lõigul asub parabool sirgest kõrgemal ja seetõttu tuleb sellest lahutada
Valmis lahendus võib välja näha selline:
Soovitud figuuri piirab ülaltoodud parabool ja allpool sirgjoon.
Segmendil vastavalt vastavale valemile:
Vastus:
Näide 4
Arvutage joonise pindala, mis on piiratud joontega , , , .
Lahendus: Kõigepealt teeme joonise:
Kuju, mille ala peame leidma, on sinise varjundiga(vaadake hoolikalt seisukorda - kuidas figuur on piiratud!). Kuid praktikas juhtub tähelepanematuse tõttu sageli "tõrge", et peate leidma roheliseks varjutatud figuuri ala!
See näide on kasulik ka selle poolest, et see arvutab kujundi pindala kahe kindla integraali abil.
Tõesti:
1) Lõigul telje kohal on sirge graafik;
2) Lõigul telje kohal on hüperbooli graafik.
On üsna ilmne, et piirkondi saab (ja tuleks) lisada, seega:
Hakkame kaaluma topeltintegraali arvutamise tegelikku protsessi ja tutvume selle geomeetrilise tähendusega.
Topeltintegraal on arvuliselt võrdne tasapinnalise joonise pindalaga (integratsioonipiirkond). See on topeltintegraali kõige lihtsam vorm, kui kahe muutuja funktsioon on võrdne ühega: .
Esiteks vaatame probleemi üldises vormis. Nüüd olete üsna üllatunud, kui lihtne kõik tegelikult on! Arvutame tasase kujundi pindala, mis on piiratud joontega. Kindluse huvides eeldame, et segmendil . Selle joonise pindala on arvuliselt võrdne:
Kujutame ala joonisel: 
Valime ala läbimiseks esimese viisi: 
Seega: 
Ja kohe oluline tehniline tehnika: itereeritud integraale saab arvutada eraldi. Kõigepealt sisemine integraal, seejärel välimine integraal. Soovitan seda meetodit selle teema algajatele.
1) Arvutame sisemise integraali ja integreerimine toimub muutuja “y” kaudu: 
Määramatu integraal on siin kõige lihtsam ja siis kasutatakse banaalset Newtoni-Leibnizi valemit, ainsa erinevusega, et integreerimise piirid ei ole numbrid, vaid funktsioonid. Esiteks asendasime ülemise piiri "y"-ga (antiderivatiivne funktsioon), seejärel alumine piir
2) Esimeses lõigus saadud tulemus tuleb asendada välisintegraaliga: 
Kogu lahenduse kompaktsem esitus näeb välja järgmine:
Saadud valem 
on täpselt töövalem tasapinnalise kujundi pindala arvutamiseks "tavalise" kindla integraali abil! Vaadake õppetundi Pindala arvutamine kindla integraali abil, seal ta on igal sammul!
See on, probleem pindala arvutamisel topeltintegraali abil ei erine palju ala leidmise probleemist kindla integraali abil! Tegelikult on see sama asi!
Seetõttu ei tohiks raskusi tekkida! Ma ei vaata väga palju näiteid, kuna tegelikult olete selle ülesandega korduvalt kokku puutunud.
Näide 9
Lahendus: Kujutame ala joonisel: 
Valime ala läbimise järgmise järjekorra: 
Siin ja edasi ma ei peatu sellel, kuidas ala läbida, kuna esimeses lõigus anti väga üksikasjalikud selgitused.
Seega: 
Nagu ma juba märkisin, on algajatele parem itereeritud integraalid eraldi arvutada ja jään sama meetodi juurde:
1) Esiteks, kasutades Newtoni-Leibnizi valemit, käsitleme sisemist integraali: 
2) Esimeses etapis saadud tulemus asendatakse välise integraaliga: 
Punkt 2 on tegelikult tasapinnalise kujundi pindala leidmine kindla integraali abil.
Vastus:
See on nii rumal ja naiivne ülesanne.
Huvitav näide iseseisva lahenduse kohta:
Näide 10
Arvutage topeltintegraali abil tasapinnalise kujundi pindala, mis on piiratud joontega , ,
Lõpplahenduse ligikaudne näide tunni lõpus.
Näidetes 9-10 on palju tulusam kasutada ala läbimiseks esimest meetodit, uudishimulikud lugejad, muide, saavad läbimise järjekorda muuta ja alasid arvutada teise meetodi abil. Kui te ei eksi, saate loomulikult samad pindalaväärtused.
Kuid mõnel juhul on teine ala läbimise meetod tõhusam ja noore nohiku kursuse lõpus vaatame sellel teemal veel paari näidet:
Näide 11
Arvutage topeltintegraali abil joontega piiratud tasapinnalise kujundi pindala,
Lahendus: Ootame kahte omapäraga parabooli, mis asetsevad külili. Pole vaja naeratada, sarnased asjad esinevad üsna sageli mitmes integraalis.
Kuidas on kõige lihtsam joonistada?
Kujutagem ette parabooli kahe funktsiooni kujul:
– ülemine haru ja – alumine haru.
Samamoodi kujutage ette parabooli ülemise ja alumise kujul 
oksad.
Järgmiseks graafikureeglite punktipõhine joonistamine, mille tulemuseks on selline veider joonis: 
Arvutame joonise pindala topeltintegraali abil vastavalt valemile:
Mis juhtub, kui valime ala läbimiseks esimese meetodi? Esiteks tuleb see ala jagada kaheks osaks. Ja teiseks jälgime seda kurba pilti: 
. Integraalid pole muidugi ülikeerulise tasemega, aga... on vana matemaatiline ütlus: see, kes on juurte lähedal, ei vaja testi.
Seetõttu väljendame tingimuses antud arusaamatusest pöördfunktsioonid: 
Selle näite pöördfunktsioonide eeliseks on see, et nad määravad kogu parabooli korraga ilma lehtede, tammetõrude, okste ja juurteta.
Teise meetodi kohaselt on ala läbimine järgmine: 
Seega: 
Nagu öeldakse, tunneta erinevust.
1) Tegeleme sisemise integraaliga:
Asendame tulemuse välimise integraaliga:
Integreerimine muutuja "y" kohal ei tohiks segadust tekitada; kui oleks olemas täht "zy", oleks suurepärane integreerida selle üle. Kuigi kes loeb tunni teist lõiku Kuidas arvutada pöörleva keha ruumala, ei koge ta “Y” meetodi järgi integreerimisel enam vähimatki kohmetust.
Pöörake tähelepanu ka esimesele sammule: integrand on paaris ja integreerimise intervall on nulli suhtes sümmeetriline. Seetõttu saab segmenti poole võrra vähendada ja tulemust kahekordistada. Seda tehnikat kirjeldatakse õppetükis üksikasjalikult. Tõhusad meetodid kindla integraali arvutamiseks.
Mida lisada…. Kõik!
Vastus:
Integreerimistehnika testimiseks võite proovida arvutada . Vastus peaks olema täpselt sama.
Näide 12
Arvutage topeltintegraali abil joontega piiratud tasapinnalise kujundi pindala 
See on näide, mille saate ise lahendada. Huvitav on märkida, et kui proovite kasutada ala läbimise esimest meetodit, ei pea kujund enam kaheks, vaid kolmeks osaks jagama! Ja vastavalt saame kolm paari korduvaid integraale. Mõnikord juhtub.
Meistriklass on lõppenud ja on aeg liikuda edasi suurmeistri tasemele - Kuidas arvutada topeltintegraali? Näited lahendustest. Püüan teises artiklis mitte nii maniakaalne olla =)
Soovin teile edu!
Lahendused ja vastused:
Näide 2:Lahendus:
Kujutame piirkonda joonisel:
Valime ala läbimise järgmise järjekorra:
Seega: 
Liigume edasi pöördfunktsioonide juurde:
Seega: 
Vastus:
Näide 4:Lahendus:
Liigume edasi otseste funktsioonide juurde:
Teeme joonise:
Muudame ala läbimise järjekorda:
Vastus:
