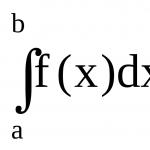Izračunavanje površine pomoću određenog integrala. Izračunavanje površina figura ograničenih datim linijama. IV. Objašnjenje novog materijala
Iz definicije slijedi da je za nenegativnu funkciju f(x) definitivni integral jednak površini krivolinijskog trapeza ograničenog krivom y = f(x), pravim linijama x = a, x = b a apscisa = 0 (slika 4.1).
Ako je funkcija – f(x) nepozitivna, onda je definitivni integral 
jednaka površini odgovarajućeg krivolinijskog trapeza, uzetog sa predznakom minus (slika 4.7).
Slika 4.7 – Geometrijsko značenje određenog integrala za nepozitivnu funkciju
Za proizvoljnu kontinuiranu funkciju f(x), definitivni integral 
jednak je zbiru površina krivolinijskih trapeza koji leže ispod grafika funkcije f(x) i iznad ose apscise, minus zbir površina krivolinijskih trapeza koji leže iznad grafika funkcije f(x) i ispod apscisa osi (slika 4.8).
Slika 4.8 – Geometrijsko značenje određenog integrala za proizvoljnu kontinuiranu funkciju f(x) (znak plus označava površinu koja se dodaje, a znak minus označava površinu koja se oduzima).
Prilikom izračunavanja površina krivolinijskih figura u praksi se često koristi sljedeća formula: 
, gdje je S površina figure zatvorene između krivulja y = f 1 (x) i y = f 2 (x) na segmentu [a,b], te f 1 (x) i f 2 (x ) su kontinuirane funkcije definirane na ovom segmentu, takve da je f 1 (x) ≥ f 2 (x) (vidi slike 4.9, 4.10).
Prilikom proučavanja ekonomskog značenja derivata, ustanovljeno je da derivat djeluje kao stopa promjene nekog ekonomskog objekta ili procesa tokom vremena ili u odnosu na drugi faktor koji se proučava. Da bi se utvrdilo ekonomsko značenje određenog integrala, potrebno je razmotriti samu brzinu kao funkciju vremena ili nekog drugog faktora. Zatim, pošto određeni integral predstavlja promenu antiderivata, dobijamo da u ekonomiji on vrednuje promenu ovog objekta (procesa) u određenom vremenskom periodu (ili uz određenu promenu drugog faktora).
Na primjer, ako funkcija q=q(t) opisuje produktivnost rada ovisno o vremenu, tada je definitivni integral ove funkcije 
predstavlja volumen izlaza Q za vremenski period od t 0 do t 1.
Metode za izračunavanje određenih integrala zasnivaju se na metodama integracije o kojima smo ranije govorili (nećemo izvoditi dokaze).
Prilikom pronalaženja neodređenog integrala koristili smo metodu promjene varijabli na osnovu formule: f(x)dx= =f((t))`(t)dt, gdje je x =(t) funkcija diferenciran na razmatrano između. Za definitivni integral, formula promjene varijable ima oblik 
, Gdje 
i za sve.
Primjer 1. Nađi
Neka je t= 2 –x 2. Tada je dt= -2xdx i xdx= - ½dt.
Kod x = 0 t= 2 – 0 2 = 2. Kod x = 1t= 2 – 1 2 = 1. Tada
Primjer 2. Nađi
Primjer 3. Nađi
Formula integracije po dijelovima za određeni integral ima oblik: 
, Gdje 
.
Primjer 1. Nađi
Neka je u=ln(1 +x),dv=dx. Onda
Primjer 2. Nađi
Izračunavanje površina ravnih figura pomoću određenog integrala
Primjer 1. Nađite površinu figure ograničene linijama y = x 2 – 2 i y = x.
Grafikon funkcije y= x 2 – 2 je parabola sa minimalnom tačkom u x= 0, y= -2; Osa apscise seku u tačkama 
. Grafikon funkcije y = x je prava linija, simetrala nenegativnog koordinatnog kvadranta.
Nađimo koordinate presječnih tačaka parabole y = x 2 – 2 i prave linije y = x rješavanjem sistema ovih jednačina:
x 2 – x - 2 = 0
x = 2; y= 2 ili x = -1;y= -1
Dakle, figura čiju površinu treba pronaći može se prikazati na slici 4.9.
Slika 4.9 – Slika ograničena linijama y = x 2 – 2 i y = x
Na segmentu [-1, 2] x ≥ x 2 – 2.
Koristimo formulu 
, stavljajući f 1 (x) = x; f 2 (x) = x 2 – 2; a= -1; b= 2.
Primjer 2. Nađite površinu figure ograničene linijama y = 4 - x 2 i y = x 2 - 2x.
Grafikon funkcije y = 4 - x 2 je parabola sa maksimalnom tačkom u x = 0, y = 4; X-osa se siječe u tačkama 2 i -2. Grafikon funkcije y = x 2 – 2x je parabola sa minimalnom tačkom na 2x- 2 = 0, x = 1, y = -1; X-osa seče u tačkama 0 i 2.
Nađimo koordinate presječnih tačaka krivih:
4 - x 2 = x 2 – 2x
2x 2 – 2x - 4 = 0
x 2 – x - 2 = 0
x = 2; y= 0 ili x = -1;y= 3
Dakle, broj čiju površinu treba pronaći može se prikazati na slici 4.10.
Slika 4.10 - Slika ograničena linijama y = 4 - x 2 i y = x 2 - 2x
Na segmentu [-1, 2] 4 - x 2 ≥ x 2 – 2x.
Koristimo formulu 
, stavljajući f 1 (x) = 4 - - x 2; f 2 (x) = x 2 – 2x;a= -1;b= 2.
Primjer 3. Pronađite površinu figure ograničene linijama y = 1/x; y= x 2 i y= 4 u nenegativnom koordinatnom kvadrantu.
Grafikon funkcije y = 1/x je hiperbola, a za pozitivno x je konveksan prema dolje; koordinatne ose su asimptote. Grafikon funkcije y = x 2 u nenegativnom koordinatnom kvadrantu je grana parabole sa minimalnom tačkom u početku. Ovi grafovi se sijeku na 1/x = x 2; x 3 = 1; x = 1; y = 1.
Grafikon funkcije y = 1/x siječe pravu liniju y = 4 na x = 1/4, a grafik funkcije y = x 2 na x = 2 (ili -2).
Dakle, figura čiju površinu treba pronaći može se prikazati na slici 4.11.
Slika 4.11 - Slika ograničena linijama y = 1/x; y= x 2 i y= 4 u nenegativnom koordinatnom kvadrantu
Potrebna površina figure ABC jednaka je razlici između površine pravokutnika ABHE, koja je jednaka 4 * (2 - ¼) = 7, i zbira površina dva krivolinijska trapeza ACFE i CBHF. Izračunajmo površinu ACFE:
Izračunajmo površinu SVNF:
.
Dakle, tražena površina je 7 – (ln4 + 7/3) = 14/3 –ln43,28 (jedinica 2).
Čas matematike za prvu godinu ustanova srednjeg stručnog obrazovanja
Predmet: "Izračunavanje površina ravnih figura pomoću određenog integrala."
Nastavnik matematike S.B. Baranova
Obrazovni ciljevi:
obezbijediti ponavljanje, generalizaciju i sistematizaciju materijala na ovu temu;
stvoriti uslove za kontrolu (samokontrolu) znanja i vještina.
Razvojni zadaci:
promoviraju formiranje vještina primjene tehnika poređenja, generalizacije i isticanja glavne stvari;
nastaviti razvoj matematičkih horizonata, mišljenja i govora, pažnje i pamćenja.
Edukativni zadaci:
promovirati interesovanje za matematiku;
obrazovanje aktivnosti, mobilnosti, komunikacijskih vještina.
Vrsta lekcije – kombinovani čas sa elementima problemskog učenja.
Nastavne metode i tehnike – problematičan, vizuelni, samostalni rad učenika, samotestiranje.
Oprema – prilog lekciji, tabele.
Plan lekcije
Organiziranje vremena. Priprema učenika za rad na času.
Priprema učenika za aktivan rad (provjera računskih vještina i tablica integrala po grupama).
Priprema za učenje novog gradiva kroz ponavljanje i ažuriranje osnovnih znanja.
Rad sa novim materijalom.
Primarno razumijevanje i primjena proučenog gradiva, njegova konsolidacija.
Zadaća.
Primena znanja.
Rezimirajući.
Refleksija.
Tokom nastave
1. Organizacioni momenat.
Koncept određenog integrala jedan je od osnovnih pojmova matematike. Do kraja 17. vijeka. Newton i Leibniz su stvorili aparat za diferencijalni i integralni račun, koji čini osnovu matematičke analize.
U prethodnim lekcijama smo naučili da „uzmemo“ neodređene integrale i izračunamo određene integrale. Ali mnogo je važnija upotreba određenog integrala. Znamo da se može koristiti za izračunavanje površina zakrivljenih trapeza. Danas ćemo odgovoriti na pitanje: "Kako to učiniti?"
2. Priprema učenika za aktivan rad.
Ali prvo moramo testirati naše računske vještine i znanje tablice integrala. Pred vama je zadatak čiji će rezultat biti izjava francuskog matematičara S.D. Poisson (Život je obogaćen za dvije stvari: raditi matematiku i podučavati je).
Zadatak se izvodi u parovima ().
3. Priprema za učenje novog gradiva kroz ponavljanje i ažuriranje osnovnih znanja.
Prijeđimo na temu naše lekcije: "Izračunavanje površina ravnih figura pomoću određenog integrala." Pored sposobnosti izračunavanja određenog integrala, moramo zapamtiti svojstva površina. Šta su oni?
Jednake figure imaju jednake površine.
Ako je figura podijeljena na dva dijela, tada se njena površina nalazi kao zbir površina pojedinih dijelova.
Također moramo ponoviti pravilo integrala zbira i Newton-Leibnizovu formulu.
4. Rad sa novim integralom
1. Definitivni integral se koristi za izračunavanje površina krivolinijskih trapeza. Ali u praksi se češće javljaju brojke koje nisu takve i moramo naučiti kako pronaći površine upravo takvih figura.
Radite prema tabeli “Osnovni slučajevi rasporeda ravnine figure i odgovarajuće formule površine” ().
2. Testirajmo se.
Rad sa zadatkom () nakon čega slijedi verifikacija (Tabela br. 3).
3. Ali sposobnost odabira pravih formula za površinu nije dovoljna. U sljedećoj tabeli () u svakom od zadataka postoji "vanjski" razlog koji ne dozvoljava izračunavanje površine figure. Hajde da ih nađemo.
a) formule za grafove funkcija nisu naznačene.
b) ne postoje granice integracije.
c) nazivi grafikona nisu naznačeni i ne postoji jedno ograničenje.
d) formula jednog od grafikona nije naznačena.
4. Uzimajući u obzir obavljeni rad, formulisaćemo i zapisati algoritam za rešavanje zadataka na temu lekcije.
Konstruirajte grafove ovih linija. Odredite željenu figuru.
Pronađite granice integracije.
Zapišite površinu željene figure koristeći određeni integral.
Izračunajte rezultujući integral.
5. Primarno razumijevanje i primjena proučenog gradiva, njegovo učvršćivanje.
1. Uzimajući u obzir algoritam, izvršimo zadatak br. 2 iz posljednje tabele.
Slika 1
Rješenje:
Za tačku A:
– ne zadovoljava uslove zadatka
Za tačku B:
– ne zadovoljava uslove problema.
odgovor: (kv. jedinice).
2. Ali prilikom izvođenja ovog zadatka algoritam nije u potpunosti primijenjen. Da bismo to riješili, izvršimo sljedeći zadatak:
Vježbajte. Pronađite površinu figure ograničenu linijama , .
Slika 2
Rješenje:
– parabola, vrh (m,n).
(0;2) – vrh
Hajde da pronađemo granice integracije.
odgovor: (kv. jedinice).
6. Domaći.
Izračunajte površinu figure ograničene linijama (rastaviti zadatak).
7. Primena znanja.
Samostalni rad (Prilog br. 5))
8. Sumiranje.
naučili da kreiraju formule za pronalaženje površina ravnih figura;
pronaći granice integracije;
izračunaj površinu figura.
9. Refleksija.
Učenicima se dijele leci. Moraju ocijeniti svoj rad odabirom jedne od ponuđenih opcija odgovora.
Procijenite stepen težine lekcije.
Na času ste imali:
lako;
obično;
teško.
U potpunosti sam ga shvatio i mogu ga primijeniti;
Savladao sam ga u potpunosti, ali mi ga je teško koristiti;
naučeno djelomično;
nisam shvatio.
Nakon uvida u odgovore izvedite zaključak o pripremljenosti učenika za praktičan rad.
rabljene knjige:
Valutse I.I., Diligulin G.D. Matematika za tehničke škole.
Kramer N.Sh., Putko B.A., Trishin I.M. Viša matematika za ekonomiste.
Danko P.E., Popov A.G. Viša matematika, 1. dio.
Zvanich L.I., Ryazanovsky A.R. M., Nova škola.
Novine “Matematika”. Izdavačka kuća “Prvi septembar”.
Dodatak br. 1
Izračunajte određene integrale i prepoznaćete jednu od tvrdnji francuskog matematičara S.D. Poissona.
9
Život
Tri
Dva
Stvari
Zanimanje
Matematika
Aritmetika
Nastava
Ona
Decorated
Zaboravljanjem
Dodatak br. 2
GLAVNI SLUČAJEVI LOKACIJE RAVNE FIGURE I ODGOVARAJUĆIH FORMULA POVRŠINA
______________________________________
_
__________________________________
______
________________________________
______
___________________________________
Figura koja je simetrična u odnosu na ordinatnu os ili ishodište.
Dodatak br. 3
Koristeći određeni integral, zapišite formule za izračunavanje površina osenčenih figura na slici.
_________________________________________
__________________________________________
___________________________________________
___________________________________________
____________________________________________
Dodatak br. 4
Pronađite "vanjski" razlog koji vam ne dozvoljava da izračunate površinu figure.
Slika 1
Slika 2
Slika 3
Slika 4
_____________________________
Dodatak br. 5
Samostalan rad
Opcija 1
Napiši koristeći integrale površine figura i izračunaj ih
Nacrtajte oblike, plčije su površine jednake sljedećim integralima:
Samostalan rad
Opcija 2
Utvrdite da li su sljedeće tvrdnje tačne:
Snimite sakoristeći integrale površine figura i izračunaj ih
Nacrtaj figure čije su površine jednake sljedećim integralima:
Definicija. Razlika F (b) – F (a) naziva se integral funkcije f (x) na intervalu [ a ; b ] i označava se na sljedeći način: = F (b) – F (a) – Newton-Leibniz formula.
Geometrijsko značenje integrala.
Područje krivolinijskog trapeza ograničenog kontinuiranim pozitivnim grafom na intervalu [a; b ] funkcije f (x), Ox os i linije x=a i x= b:
Izračunavanje površina pomoću integrala.
1. Površina figure ograničena kontinuiranim negativnim grafom na intervalu [a; b ] funkcije f (x), Ox os i linije x=a i x= b:
2. Površina figure ograničena grafovima kontinuiranih funkcija f (x) i linijama x=a, x= b:
3. Površina figure ograničena grafovima kontinuiranih funkcija f (x) i:
4. Područje figure ograničeno grafovima kontinuiranih funkcija f (x) i Ox osi:
Zadaci i testovi na temu "Integral. Izračunavanje površina pomoću integrala"
- Integral
Lekcije: 4 Zadaci: 13 Testovi: 1
- Izračunavanje površina pomoću integrala - Antiderivativ i integralni razred 11
Lekcije: 1 Zadaci: 10 Testovi: 1
- Antiderivativ - Antiderivativ i integralni razred 11
Lekcije: 1 Zadaci: 11 Testovi: 1
- Planimetrija: proračun dužina i površina
Zadaci: 7
- Izračuni i konverzije - Priprema za Jedinstveni državni ispit iz matematike Jedinstveni državni ispit iz matematike
Zadaci: 10
Prije nego počnete izračunavati površinu figure ograničene datim linijama, pokušajte prikazati ovu figuru u koordinatnom sistemu. Ovo će znatno olakšati rješavanje problema.
Proučavanje teorijskih materijala na ovu temu daje vam priliku da savladate koncepte antiderivacije i integrala, shvatite povezanost između njih, savladate najjednostavniju tehniku integralnog računa i naučite primijeniti integral na izračunavanje površina figura ograničenih grafovima funkcija. .
Primjeri.
1. Izračunajte integral
Rješenje:
odgovor: 0.
2. Pronađite površinu figure ograničenu linijama
a) f(x) = 2 X – X 2 i x-osa
Rješenje: Grafikon funkcije f(x) = 2x - x 2 je parabola. Vrh: (1; 1).
odgovor:(kv. jedinice).
Zapravo, da biste pronašli površinu figure, nije vam potrebno toliko znanja o neodređenom i određenom integralu. Zadatak „izračunati površinu pomoću određenog integrala“ uvijek uključuje izradu crteža, tako da će vaše znanje i vještine crtanja biti mnogo hitniji problem. U tom smislu, korisno je osvježiti svoje pamćenje grafova osnovnih elementarnih funkcija i, u najmanju ruku, moći konstruirati pravu liniju i hiperbolu.
Zakrivljeni trapez je ravna figura omeđena osom, pravim linijama i grafikom funkcije kontinuirane na segmentu koji ne mijenja predznak na ovom intervalu. Neka se ova figura nalazi ne manje x-osa:
Onda površina krivolinijskog trapeza numerički je jednaka određenom integralu. Svaki određeni integral (koji postoji) ima vrlo dobro geometrijsko značenje.
Sa stanovišta geometrije, definitivni integral je POVRŠINA.
To je, određeni integral (ako postoji) geometrijski odgovara površini određene figure. Na primjer, razmotrite definitivni integral. Integrand definira krivulju na ravni koja se nalazi iznad ose (oni koji žele mogu napraviti crtež), a sam definitivni integral je numerički jednak površini odgovarajućeg krivolinijskog trapeza.
Primjer 1
Ovo je tipična izjava o dodjeli. Prva i najvažnija tačka odluke je konstrukcija crteža. Štaviše, crtež mora biti konstruisan PRAVO.
Prilikom izrade crteža preporučujem sljedeći redoslijed: kao prvo bolje je konstruisati sve prave (ako postoje) i samo Onda- parabole, hiperbole, grafovi drugih funkcija. Isplativije je graditi grafove funkcija tačku po tačku.
U ovom problemu rješenje bi moglo izgledati ovako.
Nacrtajmo crtež (imajte na umu da jednačina definira os):
Na segmentu se nalazi graf funkcije iznad ose, Zbog toga:
odgovor:
Nakon što je zadatak završen, uvijek je korisno pogledati crtež i shvatiti da li je odgovor stvaran. U ovom slučaju, "na oko" brojimo broj ćelija na crtežu - pa, bit će ih oko 9, čini se da je istina. Apsolutno je jasno da ako dobijemo, recimo, odgovor: 20 kvadrata, onda je očito da je negdje napravljena greška - 20 ćelija očigledno ne staje u dotičnu cifru, najviše desetak. Ako je odgovor negativan, onda je i zadatak riješen pogrešno.
Primjer 3
Izračunajte površinu figure ograničenu linijama i koordinatnim osa.
Rješenje: Napravimo crtež:
Ako se nalazi zakrivljeni trapez ispod osovine(ili barem ne viši datu os), tada se njegova površina može pronaći pomoću formule:
U ovom slučaju:
Pažnja! Ove dvije vrste zadataka ne treba miješati:
1) Ako se od vas traži da jednostavno riješite određeni integral bez ikakvog geometrijskog značenja, onda on može biti negativan.
2) Ako se od vas traži da pronađete površinu figure pomoću određenog integrala, tada je površina uvijek pozitivna! Zato se minus pojavljuje u formuli o kojoj smo upravo govorili.
U praksi se najčešće figura nalazi i u gornjoj i u donjoj poluravni, te stoga od najjednostavnijih školskih zadataka prelazimo na sadržajnije primjere.
Primjer 4
Nađite površinu ravne figure ograničene linijama , .
Rješenje: Prvo morate završiti crtež. Uopšteno govoreći, kada konstruišemo crtež u problemima oblasti, najviše nas zanimaju tačke preseka linija. Nađimo tačke preseka parabole i prave. Ovo se može uraditi na dva načina. Prva metoda je analitička. Rješavamo jednačinu:
To znači da je donja granica integracije , a gornja granica integracije .
Ako je moguće, bolje je ne koristiti ovu metodu..
Mnogo je isplativije i brže graditi linije tačku po tačku, a granice integracije postaju jasne „sama po sebi“. Ipak, analitička metoda pronalaženja granica se ponekad mora koristiti ako je, na primjer, graf dovoljno velik, ili detaljna konstrukcija nije otkrila granice integracije (mogu biti frakcijske ili iracionalne). I mi ćemo također razmotriti takav primjer.
Vratimo se našem zadatku: racionalnije je prvo konstruirati pravu liniju pa tek onda parabolu. Napravimo crtež:
A sada radna formula: Ako postoji neka kontinuirana funkcija na segmentu veće ili jednako neke kontinuirane funkcije , tada se površina figure ograničena grafovima ovih funkcija i linijama , , može pronaći pomoću formule: 
Ovdje više ne morate razmišljati o tome gdje se figura nalazi - iznad ose ili ispod ose, i, grubo govoreći, bitno je koji je graf VEĆI(u odnosu na drugi grafikon), a koja je ISPOD.
U primjeru koji se razmatra, očito je da se na segmentu parabola nalazi iznad prave linije, te je stoga potrebno oduzeti od
Završeno rješenje može izgledati ovako:
Željena figura ograničena je parabolom iznad i pravom linijom ispod.
Na segmentu, prema odgovarajućoj formuli:
odgovor:
Primjer 4
Izračunajte površinu figure ograničene linijama , , , .
Rješenje: Prvo, napravimo crtež:
Figura čiju oblast treba da pronađemo je zasenčena plavom bojom(pogledajte pažljivo stanje - koliko je broj ograničen!). Ali u praksi, zbog nepažnje, često se javlja "kvar" da morate pronaći površinu figure koja je zasjenjena zelenom bojom!
Ovaj primjer je također koristan po tome što izračunava površinu figure koristeći dva određena integrala.
Zaista:
1) Na segmentu iznad ose nalazi se grafik prave linije;
2) Na segmentu iznad ose nalazi se graf hiperbole.
Sasvim je očigledno da se područja mogu (i trebaju) dodati, dakle:
Počinjemo razmatrati stvarni proces izračunavanja dvostrukog integrala i upoznati se s njegovim geometrijskim značenjem.
Dvostruki integral je numerički jednak površini ravne figure (područje integracije). Ovo je najjednostavniji oblik dvostrukog integrala, kada je funkcija dvije varijable jednaka jednoj: .
Prvo, pogledajmo problem u općem obliku. Sada ćete biti prilično iznenađeni koliko je sve zaista jednostavno! Izračunajmo površinu ravne figure ograničene linijama. Radi određenosti, pretpostavljamo da je na segmentu . Površina ove figure je brojčano jednaka:
Opišimo područje na crtežu: 
Odaberimo prvi način za prelazak područja: 
ovako: 
I odmah važna tehnička tehnika: iterirani integrali se mogu posebno izračunati. Prvo unutrašnji integral, pa spoljni integral. Toplo preporučujem ovu metodu početnicima u ovoj temi.
1) Izračunajmo unutrašnji integral, a integracija se vrši preko varijable “y”: 
Neodređeni integral je ovdje najjednostavniji, a zatim se koristi banalna Newton-Leibnizova formula, s jedinom razlikom da granice integracije nisu brojevi, već funkcije. Prvo smo zamijenili gornju granicu u “y” (antiderivativna funkcija), a zatim donju granicu
2) Rezultat dobijen u prvom paragrafu mora se zamijeniti eksternim integralom: 
Kompaktniji prikaz cjelokupnog rješenja izgleda ovako:
Rezultirajuća formula 
je upravo radna formula za izračunavanje površine ravne figure pomoću "običnog" određenog integrala! Gledajte lekciju Izračunavanje površine pomoću određenog integrala, tu je na svakom koraku!
To je, problem izračunavanja površine pomoću dvostrukog integrala nije mnogo drugačije iz problema pronalaženja površine pomoću određenog integrala! U stvari, to je ista stvar!
Shodno tome, ne bi trebalo biti nikakvih poteškoća! Neću se osvrtati na mnogo primjera, jer ste se vi, zapravo, više puta susreli s ovim zadatkom.
Primjer 9
Rješenje: Opišimo područje na crtežu: 
Odaberemo sljedeći redoslijed obilaženja područja: 
Ovdje i dalje neću se zadržavati na tome kako preći područje, jer su u prvom pasusu data vrlo detaljna objašnjenja.
ovako: 
Kao što sam već napomenuo, za početnike je bolje da izračunaju iterirane integrale odvojeno, a ja ću se držati iste metode:
1) Prvo, koristeći Newton-Leibniz formulu, bavimo se unutrašnjim integralom: 
2) Rezultat dobiven u prvom koraku zamjenjuje se u eksterni integral: 
Tačka 2 je zapravo pronalaženje površine ravne figure pomoću određenog integrala.
odgovor:
Ovo je tako glup i naivan zadatak.
Zanimljiv primjer za samostalno rješenje:
Primjer 10
Koristeći dvostruki integral, izračunajte površinu ravne figure ograničene linijama , ,
Približan primjer konačnog rješenja na kraju lekcije.
U primjerima 9-10 mnogo je isplativije koristiti prvu metodu prelaska područja; radoznali čitatelji, inače, mogu promijeniti redoslijed obilaska i izračunati površine pomoću druge metode. Ako ne pogriješite, tada ćete, naravno, dobiti iste vrijednosti površine.
Ali u nekim slučajevima, drugi način prelaska područja je učinkovitiji, a na kraju tečaja za mlade štrebere, pogledajmo još nekoliko primjera na ovu temu:
Primjer 11
Koristeći dvostruki integral, izračunajte površinu ravne figure ograničene linijama,
Rješenje: Radujemo se dvije parabole s quirk koje leže na njihovim stranama. Nema potrebe da se smiješite, slične stvari se često dešavaju u više integrala.
Kako je najlakše napraviti crtež?
Zamislimo parabolu u obliku dvije funkcije:
– gornja grana i – donja grana.
Slično, zamislite parabolu u obliku gornjeg i donjeg 
grane.
Zatim, crtanje pravila grafova po tačkama, što rezultira tako bizarnom figurom: 
Izračunavamo površinu figure pomoću dvostrukog integrala prema formuli:
Šta će se dogoditi ako odaberemo prvi način prelaska područja? Prvo, ovo područje će se morati podijeliti na dva dijela. I drugo, posmatraćemo ovu tužnu sliku: 
. Integrali, naravno, nisu na nekom superkomplikovanom nivou, ali... postoji stara matematička izreka: onima koji su blizu korena nije potreban test.
Stoga, iz nesporazuma datog u uvjetu, izražavamo inverzne funkcije: 
Inverzne funkcije u ovom primjeru imaju prednost što određuju cijelu parabolu odjednom bez ikakvih listova, žira, grana i korijena.
Prema drugoj metodi, obilazak područja će biti sljedeći: 
ovako: 
Kako kažu, osjetite razliku.
1) Bavimo se unutrašnjim integralom:
Zamjenjujemo rezultat u vanjski integral:
Integracija preko varijable “y” ne bi trebala biti zbunjujuća; da postoji slovo “zy”, bilo bi sjajno integrirati preko njega. Mada ko je pročitao drugi pasus lekcije Kako izračunati zapreminu tela rotacije, on više ne doživljava ni najmanju nespretnost sa integracijom po "Y" metodi.
Obratite pažnju i na prvi korak: integrand je paran, a interval integracije je simetričan oko nule. Dakle, segment se može prepoloviti, a rezultat se može udvostručiti. Ova tehnika je detaljno komentarisana u lekciji. Efikasne metode za izračunavanje određenog integrala.
Šta dodati…. Sve!
odgovor:
Da biste testirali svoju tehniku integracije, možete pokušati izračunati . Odgovor bi trebao biti potpuno isti.
Primjer 12
Koristeći dvostruki integral, izračunajte površinu ravne figure ograničene linijama 
Ovo je primjer koji možete sami riješiti. Zanimljivo je primijetiti da ako pokušate koristiti prvi način prelaska područja, figura više neće morati biti podijeljena na dva, već na tri dijela! I, shodno tome, dobijamo tri para ponovljenih integrala. Ponekad se to desi.
Majstorska klasa je privedena kraju i vrijeme je da pređemo na velemajstorski nivo - Kako izračunati dvostruki integral? Primjeri rješenja. Pokušaću da ne budem toliko manijalan u drugom članku =)
Želim ti uspjeh!
Rješenja i odgovori:
Primjer 2:Rješenje:
Oslikajmo područje na crtežu:
Odaberemo sljedeći redoslijed obilaženja područja:
ovako: 
Pređimo na inverzne funkcije:
ovako: 
odgovor:
Primjer 4:Rješenje:
Pređimo na direktne funkcije:
Napravimo crtež:
Promijenimo redoslijed prelaska područja:
odgovor:
